Decimal number system, binary octal and hexadecimal

Decimal number system, binary octal and hexadecimal

Systems binary and hexadecimal counts are widely used in the fields of electronics and computers . Any programmer must know in addition to decimal and octal systems.

Principle of base

The base is the number used to define a numbering system .
The basis of the decimal system is ten whereas the eight octal system .
Whatever the used numerical basis , it follows the following relationship :

or : b_i: figure based on rank i
and : aⁱ : power base exponent of rank i

Example: base 10
1986 = (1 x 10³) + (9 x 10²) + (8 x 10¹) + (6 x 10⁰)

The decimal system

The decimal system is one in which we have the habit of writing .
Each digit can have 10 different values:
0 , 1 , 2, 3 , 4, 5 , 6 , 7 , 8, 9 , therefore , the base for a decimal system is 10 .
Everything written in the decimal number system satisfies the following relationship :
745 = 7 x 100 + 4 x 10 + 5 x 1
745 = 7 x 10 x 10 + 4 x 10 + 1 x 5
745 = 7 x 10² + 4 x 10¹ + 5 x 10⁰

Each digit of the number is multiplied by a power of 10 : the weight of the number.

The exponent of this power is zero for the digit furthest to the right and increases by one for each pass one digit to the left.
12 435 = 1 x 10⁴ + 2 x 10³ + 4 x 10² + 3 x 10¹ + 5 x 10⁰
This way of writing numbers is called numbering system position.
In our conventional system, we use powers of 10 to weigh the value of numbers according to their position , however it is possible to imagine other number systems having as a basis a different integer.

The octal system

The octal system uses a number system having as base 8 (octal = > Latin octo = eight) .
It should be noted that in this system we will have 10 symbols, but only 8 :
0 , 1 , 2, 3 , 4, 5 , 6 , 7
Thus, a number expressed in base 8 can be presented as follows :
(745)₈
When a number is written , it will be clear the database in which it is expressed to remove any indeterminacy ( 745 also available in base 10) .
Thus, the number will be in parentheses ( 745 in our example) and indexed a number representing its base ( 8 subscript ) .

This base obey the same rules as the base 10, seen above , and we can decompose (745)₈ as follows :
(745)₈ = 7 x 8² + 4 x 8¹ + 5 x 8⁰
(745)₈ = 7 x 64 + 4 x 8 + 5 x 1
(745)₈ = 448 + 32 + 5
We have seen that :

(745)₈ = (485)₁₀.

The binary system

In the binary system, each digit can have two different values ​​: 0 , 1.
Thus , the system 2 is based .
Everything about this number system satisfies the following relationship :

10 110)₂ = 1 x 2⁴ + 0 x 2³ + 1 x 2² + 1 x 2¹ + 0 x 2⁰
(10 110)₂ = 1 x 16 + 0 x 8 + 1 x 4 + 1 x 2 + 0 x 1
So : (10110)₂ = (22)₁₀

All numbering systems position obey the rules we have just seen .

The hexadecimal system

The hexadecimal system uses the following 16 symbols :
0 , 1 , 2, 3 , 4, 5 , 6 , 7 , 8, 9, A , B , C , D , E, F.
Therefore , the system 16 is based .
A number expressed in base 16 can be presented as follows :
(5AF)₁₆
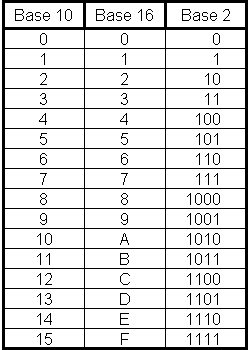
The correspondence between base 2, base 10 and base 16 is indicated in the table below :

The number (5AF)₁₆ can be decomposed as follows :
(5AF)₁₆ = 5 x 16² + A x 16¹ + F x 16⁰
Replacing A and F by their equivalent in base 10 , we obtain:
(5AF)₁₆ = 5 x 16² + 10 x 16¹ + 15 x 16⁰
(5AF)₁₆ = 5 x 256 + 10 x 16 + 15 x 1
So = (5AF)₁₆ = (1455)₁₀